Question

A circular bird feeder 19.0 cm in radius has rotational inertia 0.130 kg·m2. It's suspended by a thin wire and is spinning slowly at 24.2 rpm. A 173–g bird lands on the feeder's rim, coming in tangent to the rim at 1.20 m/s in a direction opposite the feeder's rotation. What's the rotation rate (in rpm) after the bird lands? (You do not need to enter any units.)

Answer 1

N₂=20.05 rpm

Step-by-step explanation:

Given that

R= 19 cm

I=0.13 kg.m²

N₁ = 24.2 rpm

`\omega_1=(2\pi * 24.2)/(60)\ rda/s`

ω₁= 2.5 rad/s

m= 173 g = 0.173 kg

v=1.2 m

Initial angular momentum L₁

L₁ = Iω₁ - m v r ( negative sign because bird coming opposite to motion of the wire motion)

Final linear momentum L₂

L₂= I₂ ω₂

I₂ = I + m r²

The is no any external torque that is why angular momentum will be conserve

L₁ = L₂

Iω₁ - m v r = I₂ ω₂

Iω₁ - m v r = ( I + m r²) ω₂

Now by putting the all values

Iω₁ - m v r = ( I + m r²) ω₂

0.13 x 2.5 - 0.173 x 1.2 x 0.19 = ( 0.13 + 0.173 x 0.19²) ω₂

0.325 - 0.0394 = 0.136 ω₂

ω₂ = 2.1 rad/s

`\omega_2=(2\pi * N_2)/(60)`

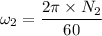
N₂=20.05 rpm