Answer: (0.7478, 0.9522)
Explanation:
We know that the confidence interval for population proportion is given by :-
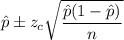
, where n= sample size.
 = sample proportion.
= sample proportion.
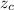 = Two -tailed z-value for confidence level of c
= Two -tailed z-value for confidence level of c
Let p be the population proportion of them that are involved in an after school activity.
As per given , we have
n= 81
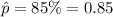
By using z-value table, Two -tailed z-value for 99% confidence

Then, the 99% confidence interval that estimates the proportion of them that are involved in an after school activity will be :-

Hence, the 99% confidence interval that estimates the proportion of them that are involved in an after school activity= (0.7478, 0.9522)