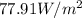Question

A vertically polarized beam of light of intensity 100 W/m2 passes through two ideal polarizers. The transmission axis of the first polarizer makes an angle of 20.0° with the vertical, and the transmission axis of the second one makes an angle of 40.0° with the vertical. What is the intensity of the light after it has passes through both polarizers?

Answer 1

To solve the problem it is necessary to apply the Malus Law. Malus's law indicates that the intensity of a linearly polarized beam of light, which passes through a perfect analyzer with a vertical optical axis is equivalent to:

`I=I_0 cos^2\theta`

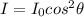
Where,

`I_ {0}` indicates the intensity of the light before passing through the polarizer,

I is the resulting intensity, and

`\theta` indicates the angle between the axis of the analyzer and the polarization axis of the incident light.

Since we have two objects the law would be,

`I=I_0cos^2\theta_1*cos^2(\theta_2-\theta_1)`

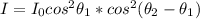
Replacing the values,

`I=100*cos^2(20)*cos^2(40-20)`

`I=100*cos^4(20)`

`I=77.91W/m^2`

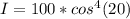
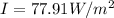
Therefore the intesity of the light after it has passes through both polarizers is
`77.91W/m^2`