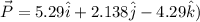To solve the problem it is necessary to apply the concepts related to the conservation of linear Moment, that is to say
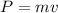
Where,
m = Mass
v = Velocity
P = Linear momentum
For the given data we have to:
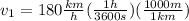
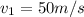
The components of this force would be given by,
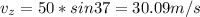
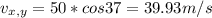 According to the definition given at the end of the problem, this component corresponds to that expressed for x and y.
According to the definition given at the end of the problem, this component corresponds to that expressed for x and y.
Applying the previous equation we have,
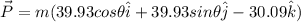
Note: The component at this direction must also decomposed
The mass is 143g=0.143kg, then:
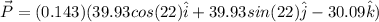
Therefore the final vector is: