Question

It costs 14 dollars to manufacture and distribute a backpack. If the backpacks sell at x dollars​ each, the number​ sold, n, is given by n equals StartFraction 2 Over x minus 14 EndFraction plus 5 (100 minus x ). Find the selling price that will maximize profit.

Answer 1

Selling price that will maximize profit is $57

Step-by-step explanation:

Given;

Costs to manufacture and distribute a backpack = $14

Number​ sold, n =
`(2)/(x-14)+5(100-x)`

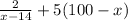
here, x is the selling cost of the bag

Now,

Profit = Total revenue - Total cost

or

P = nx - 14n

or

P = n(x - 14)

or

P =
`[(2)/(x-14)+5(100-x)]*(x-14)`

or

P = 2 + 5(100 - x)(x - 14)

or

P = 2 + 5(100x - 1400 - x² + 14x)

differentiating with respect to x

we get

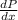`(dP)/(dx)` = 0 + 5(100 - 0 - 2x + 14)

or

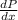`(dP)/(dx)` = 5(114 - 2x)

put

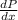`(dP)/(dx)` = 0 for point of maxima or minima

5(114 - 2x) = 0

or

114 - 2x = 0

or

x = $57

Now,

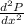`(d^2P)/(dx^2)` = 5(0 - 2) = -10

[hence, negative result means x = 57 is point of maxima]

Therefore,

Selling price that will maximize profit is $57