Question

A civil engineer is analyzing the compressive strength of concrete. Compressive strength is approximately normally distributed with variance σ2 = 800 psi2. It is desired to estimate the compressive strength with an error that is less than 13 psi at 95% confidence. What sample size is required? Round your answer up to the nearest whole number. The answer must be exact.

Answer 1

19

Step-by-step explanation:

The minimum sample size is given by

`p(|x\bar-\mu|<E) \geq 1-\alpha P(\frac {x\bar-\mu}{\frac {\sigma}{\sqrt n}}<-\frac {E}{\frac {\sigma}{\sqrt n}} \leq \frac {\alpha}{2})`

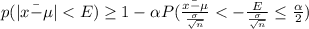
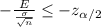`-\frac {E}{\frac {\sigma}{\sqrt n}} \leq -z_(\alpha/2)` hence making n the subject

`n \geq (\frac {z_(\alpha/2)* \sigma}{E})^(2)`

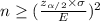
Standard deviation,
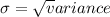`\sigma=\sqrt variance` hence
`\sigma=\sqrt 800`

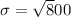
Significance level,
`\alpha`=1-Confidence=1-0.95=0.05

Critical value=
`z_(\apha/2)=z_(0.025)` and from z table the critical value is 1.96

`n \geq (\frac {z_(\alpha/2)* \sigma}{E})^(2)=(\frac {1.96* \sqrt 800}{13})^(2)= 18.18509\approx 19`

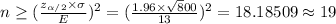
The minimum n has to be an integer hence we round it off to the nearest whole number