Question

A band is marching in a rectangular formation with dimensions n-2 and n + 8. In the second stage of their performance, they re-arrange to form a different rectangle with dimensions n and 2n - 3, excluding all the drummers. If there are at least 4 drummers, then find the sum of all possible values of n?

Answer 1

The sum of all possible values of n is 9.

Explanation:

We are going to solve this problem by subtracting areas.

For the first stage, the rectangular area of the formation is :

`(n-2).(n+8)`

In the second stage, the rectangular area of the formation is :

`n(2n-3)`

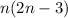
We know that in this second formation they excluded all the drummers and also we know that there are at least 4 drummers.

Therefore, the difference between the areas of the first and the second formation is :

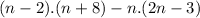`(n-2).(n+8)-n.(2n-3)` and this area must be at least 4 (because of the drummers excluded)

`(n-2).(n+8)-n.(2n-3)\geq 4`

`n^(2)+8n-2n-16-2n^(2)+3n\geq  4`

`-n^(2)+9n-16\geq  4`

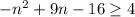
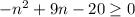`-n^(2)+9n-20\geq  0` (I)

We need to solve this and find the possibles ''n'' that satisfy the inequality.

First we look for the values that satisfy

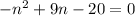`-n^(2)+9n-20=0` (II)

Using the quadratic equation :

`n_(1)=4\\n_(2)=5`

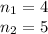
For this values of ''n'' the inequality (I) is satisfied.

Now we study the vertex.

Given a quadratic function
`f(x)=ax^(2)+bx+c`

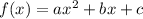
The coordinate ''x'' of the vertex is
`(-b)/(2a)`

For (II)

`a=-1\\b=9\\c=-20`

`(-b)/(2a)=(-9)/(2(-1))=(9)/(2)=4.5`

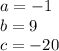
This is the coordinate ''x'' of the vertex.

For the coordinate ''y'' we calculate
`f(xVertex)`

`f(4.5)=-(4.5)^(2)+9(4.5)-20=0.25`

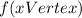
That is positive. The coordinates of the vertex are
`(4.5,0.25)`

In the quadratic function
`a=-1\\a<0`

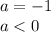
So it is a negative quadratic function.

We conclude that for the interval

[4,5] the quadratic function is positive, therefore between [4,5] the inequality (I) is satisfied.

The two possible values for n are 4 and 5.

Finally,
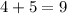`4+5=9` is the sum of all possible values of n

(Notice that n must be an integer number)