Question

A electronics manufacturer has developed a new type of remote control button that is designed to operate longer before failing to work consistently. A random sample of 23 of the new buttons is selected and each is tested in continuous operation until it fails to work consistently. The resulting lifetimes are found to have a sample mean of x¯ = 1274.2 hours and a sample standard deviation of s = 114. Independent tests reveal that the mean lifetime of the best remote control button on the market is 1210 hours. Conduct a hypothesis test to determine if the new button's mean lifetime exceeds 1210 hours. Round all calculated answers to four decimal places.

Answer 1

Claim : if the new button's mean lifetime exceeds 1210 hours.

`H_0:\mu = 1210\\H_a:\mu > 1210`

Sample mean =
`\bar{x}=1274.2`

Sample standard deviation s = 114

n = 23

Since n < 30 and sample standard deviation is given .

So, we will use t test

Formula :
`t=(x-\mu)/((s)/(√(n)))}`

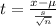
Substitute the values :

`t=(1274.2-1210)/((114)/(√(23)))`

`t=2.7008`

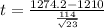
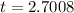
degree of freedom = n-1 = 23-1 =22

confidence level = 95%

Significance level = 5%

`t_{df,(\alpha)/(2)}=t_{22,(0.05)/(2)}=1.7170`

t calculated > t critical

So, we failed to accept null hypothesis

Thus the new button's mean lifetime exceeds 1210 hours.