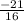Answer:
θ is decreasing at the rate of
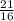 units/sec
units/sec
or
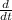 (θ) =
(θ) =
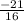
Explanation:
Given :
Length of side opposite to angle θ is y
Length of side adjacent to angle θ is x
θ is part of a right angle triangle
At this instant,
x = 8 ,
 = 7
= 7
(
 denotes the rate of change of x with respect to time)
denotes the rate of change of x with respect to time)
y = 8 ,
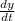 = -14
= -14
( The negative sign denotes the decreasing rate of change )
Here because it is a right angle triangle,
tanθ =
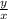 -------------------------------------------------------------------1
-------------------------------------------------------------------1
At this instant,
tanθ =
 = 1
= 1
Therefore θ = π/4
We differentiate equation (1) with respect to time in order to obtain the rate of change of θ or
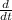 (θ)
(θ)
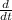 (tanθ) =
(tanθ) =
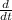 (y/x)
(y/x)
( Applying chain rule of differentiation for R.H.S as y*1/x)
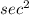 θ
θ
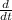 (θ) =
(θ) =
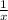
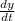 -
-
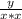
 -----------------------2
-----------------------2
Substituting the values of x , y ,
 ,
,
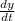 , θ at that instant in equation (2)
, θ at that instant in equation (2)
2
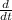 (θ) =
(θ) =
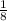 *(-14)-
*(-14)-
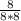 *7
*7
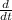 (θ) =
(θ) =
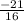
Therefore θ is decreasing at the rate of
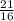 units/sec
units/sec
or
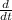 (θ) =
(θ) =