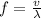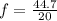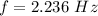Question

Laura and Elana are discussing how to solve the following problem: "A canary sits 10 m from the end of a 30-m-long clothesline, and a grackle sits 5 m from the other end. The rope is pulled by two poles that each exert a 200-N force on it. The mass per unit length is 0.10 kg/m. At what frequency must you vibrate the line in order to dislodge the grackle while allowing the canary to sit undisturbed?"

Answer 1

`f=2.236\ Hz`

Step-by-step explanation:

Given:

Length of a rope,
`l=30\ m`

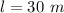
Position of Canary on the rope from one end,
`l_c=10\ m`

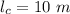
Position of Grackle on the rope from another end,
`l_g=5\ m`

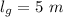
Tension in the rope,
`F_T=200\ N`

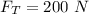
linear mass distribution on the rope,
`\mu=0.1\ kg.m^(-1)`

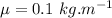
We have for the speed of wave on the string:

`v^2=(F_T)/(\mu)`

`v^2=(200)/(\0.1)`

`v=44.7\ m.s^(-1)`

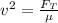
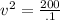
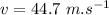
For canary to be undisturbed we need a node at this location.

Also, at the end close to Canary there must be a node to avoid any change in pattern of vibration.

So,

the distance between Canary and the closer end must be equal to half the wavelength.

`(\lambda)/(2) =10\ m`

`\Rightarrow \lambda=20\ m`

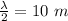
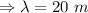
∴Wavelength of wave to be produced = 20 m. This will give us nodes at the multiples of 10 and anti-nodes at the multiples of 5.

Now, frequency:

`f=(v)/(\lambda)`

`f=(44.7)/(20)`

`f=2.236\ Hz`