Answer:
The top speed of William's boat was 45 mph
Explanation:
Let
x -----> represent the rate of the boat in still water in mph
we know that
The speed or rate is equal to divide the distance by the time
speed=distance /time
time=distance/speed
Downstream
speed=(30+x) mph
distance=10 mi
time1=10/(30+x)
Upstream
speed=(x-30) mph
distance=2 mi
time2=2/(x-30)
The sum of the time downstream plus the time upstream must be equal to 16 minutes
Convert minutes to hours
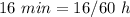
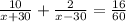
Multiply by (x+30)(x-30) both sides

Multiply by 60 both sides
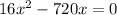
Divide by 16 both sides

The solution is x=45\ mph