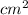Answer:
Question-6;
The value of
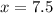
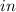
Question-7;
So the Answer is 'A'
Explanation:
Question-6;
From the portion 'ABCD';
Given the area of rectangle 'ABCD' is

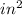 ,
,
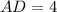
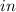 and
and
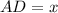
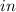
We have the formula to find the area of rectangle;
Area of rectangle 'ABCD'
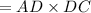
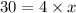
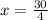
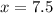
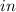
So the value of
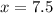
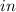 .
.
Question-7;
From figure;
Given;
All values

 ,
,

 ,
,
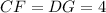
 ,
,
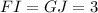
 and
and
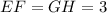

In Rectangle 'ABIJ' have three sub-rectangle which are 'ABCD' , 'CDFG' and 'FGIJ'
Area of Rectangle 'ABIJ' equal to sum of area of Rectangle 'ABCD' , area of Rectangle 'CDFG' and area of Rectangle 'FGIJ'
Area of Rectangle 'ABIJ'

Plug all values in above equation,
Area of Rectangle 'ABIJ'

Area of Rectangle 'ABIJ'
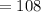
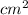
Also from figure;
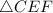 and
and
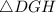 have same Area.
have same Area.
Total Area of this two triangle
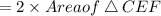
Total Area of this two triangle
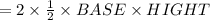
Total Area of this two triangle
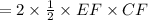
Plug 'EF' and 'CF' values in above equation,
Total Area of this two triangle

Total Area of this two triangle
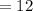
∴ Total surface area of the building block is