Question

Which best proves why the expressions 4(x+3)+2x and 6(x+2) must be equivalent expressions?

When x 3, both expressions have a value of 30.
When - 5. both expressions have a value of 42
When x 1. both expressions have a value of 18, and when x 8, both expressions have a value of 60.
When - 2. both expressions have a value of 15, and when x-6, both expressions have a value of 39.

Answer 1

The answer is C, when x 1. both expressions have a value of 18, and when x 8, both expressions have a value of 60.

Answer 2

When
`x= 3`, both expressions have a value of 30.

When
`x= 1`. both expressions have a value of 18, and when
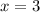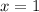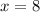`x= 8`, both expressions have a value of 60.

Explanation:

Given:

`4(x+3)+2x = 6(x+2)`

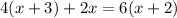
Solving the equation further we get:

`4(x+3)+2x= 6(x+2)\\ 4x+12+2x=6x+12\\6x+12=6x+12 \ \ \ \ equation \ 1`

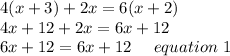
Now, When
`x=3`, both expressions have a value of 30.

Substituting Value of x in equation 1 we get,

`6x+12=6x+12\\6* 3+12 = 6* 3+12\\18+12=18+12\\30=30`

Hence the above Statement proves as Correct with given values.

Now, When
`x=-5`, both expressions have a value of 42.

Substituting Value of x in equation 1 we get,

`6x+12=6x+12\\6* -5+12 = 6* -5+12\\-30+12=-30+12\\-18=-18`

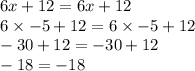
Hence the above Statement does not proves as Correct with given values.

Now,When
`x=1`, both expressions have a value of 18, and when
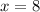`x=8`, both expressions have a value of 60.

Substituting Value of x in equation 1 we get,

`6x+12=6x+12\\6* 1+12 = 6* 1+12\\6+12=6+12\\18=18`

`6x+12=6x+12\\6* 8+12 = 6* 8+12\\48+12=48+12\\60=60`

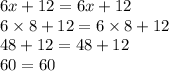
Hence the above Statement proves as Correct with given values.

When
`x=-2`. both expressions have a value of 15, and when
`x=-6`, both expressions have a value of 39.

Substituting Value of x in equation 1 we get,

`6x+12=6x+12\\6* -2+12 = 6* -2+12\\-12+12=-12+12\\0=0`

`6x+12=6x+12\\6* -6+12 = 6* -6+12\\-36+12=-36+12\\-24=-24`

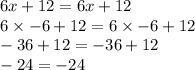
Hence the above Statement does not proves as Correct with given values.