Question

A genetic experiment involving peas yielded one sample of offspring consisting of 430 green peas and 155 yellow peas. Use a 0.05 significance level to test the claim that under the same circumstances, 24% of offspring peas will be yellow. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, conclusion about the null hypothesis, and final conclusion that addresses the original claim. Use the P-value method and the normal distribution as an approximation to the binomial distribution.

What are the null and alternative hypothesis?
What is the test statistic?
What is the P-value?
What is the conclusion about the null hypothesis?
What is the final conclusion?

Answer 1

the null and alternative hypothesis are

`H_(0)`: p=0.24

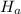`H_(a)`: p≠0.24

Test statistic is 1.416.

P-Value is 0.1568

We fail to reject the null hypothesis under 0.05 significance level

At 0.05 significance we cannot say that the proportion of offspring peas will be yellow is not 0.24 (24%)

Explanation:

Let p be the proportion of offspring peas will be yellow. Then,

`H_(0)`: p=0.24

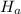`H_(a)`: p≠0.24

test statistic can be calculated as

z=
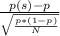`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of yellow offspring peas (
  `(155)/(155+430) =0.265`
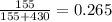
• p is the proportion of yellow offspring peas assumed under null hypothesis. (0.24)

• N is the sample size (585)

Test statistic is z=
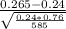`\frac{0.265-0.24}{\sqrt{(0.24*0.76)/(585) } }` ≈ 1.416.

Using z-table, we can find that P-Value is 0.1568

We fail to reject the null hypothesis under 0.05 significance level since 0.157>0.05

We can conclude that at 0.05 significance we cannot say that the proportion of offspring peas will be yellow is not 0.24 (24%)