Question

According to an​ airline, flights on a certain route are on time 8080​% of the time. Suppose 1111 flights are randomly selected and the number of​ on-time flights is recorded. ​(a) Explain why this is a binomial experiment. ​(b) Find and interpret the probability that exactly 99 flights are on time. ​(c) Find and interpret the probability that fewer than 99 flights are on time. ​(d) Find and interpret the probability that at least 99 flights are on time. ​(e) Find and interpret the probability that between 77 and 99 ​flights, inclusive, are on time.

Answer 1

a. This experiment satisfy the conditions below.

b. 0

c. 0

d. 1

e. 0

Explanation:

a. This experiment satisfy the following conditions:

1. The experiment consists of n = 1111 identical trials, i.e., to determine if each flight is on-time or not.

2. Each trial results in success or failure, i.e., the flight is on-time or not.

3. The probability of success in each trial is the same, p = 0.8, because a flight is on-time 80% of the time.

4. The trials are independent because the 1111 flights were selected randomly.

5. Te random variable of interest is Y, the number of on-time flights observed in the n = 1111 flights.

b. P(Y = 99) =
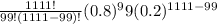`(1111!)/(99!(1111-99)!)(0.8)^99(0.2)^(1111-99)` = 0. This is the probability that 99 flights are on time and 1012 are not.

c. P(Y < 99) =
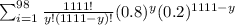`\sum_(i=1)^(98)(1111!)/(y!(1111-y)!)(0.8)^y(0.2)^(1111-y)` = 0. This is the probability that 0 flights are on-time or 1 flight is on-time or ... or 98 flights are on-time.

d. 1 - P(Y < 99) = 1 - 0 = 1. This is the probability that 99 flights are on-time or 100 flights are on-time or ... or all 1111 flights are on-time.

e.
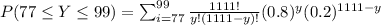`P(77\leq Y \leq 99) = \sum_(i=77)^(99)(1111!)/(y!(1111-y)!)(0.8)^y(0.2)^(1111-y)` = 0 This is the probability that 77 flights are on-time or 78 flights are on-time or ... or 99 flights are on-time.