The slope of the ramp is
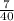 if two beams are apart at 40 feet and at heights of 3.5 feet and 10.5 feet respectively.
if two beams are apart at 40 feet and at heights of 3.5 feet and 10.5 feet respectively.
Explanation:
The two beams are 40 feet apart this is the horizontal distance.
As per the given question 3.5 feet beam is at initial point that is
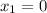 and beams are apart 40 feet that is
and beams are apart 40 feet that is
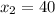 .
.
Vertical distance is the heights of the beam are
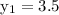 feet and other bean is
feet and other bean is

To find the slope of the ramp we know that, slope is the ratio of the vertical change to the horizontal change.
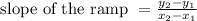
Substitute the values
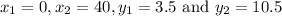 in the above formula.
in the above formula.
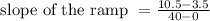
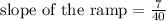
Thus by using the slope formula we found that slope of the ramp for the given conditions is
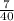 .
.