a) 90% confidence interval is (440.426, 591.574)
b) The range of values that, with a certain degree of confidence, represent the true value of the population parameter is known as the confidence interval. Option a is the right choice.
As per the given information,
Sum of the data is 8,772
The sample size is n =17.
Sample mean formula is as follows:
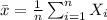
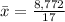
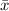 = 516
= 516
The population standard deviation is σ = 190.
The 100(1-a)% confidence interval for the population mean when the population standard deviation is known is given by,
CI = Point estimate+Margin of error
CI =
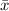 ±
±
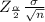
The confidence level is 90%.
Thus, the level of significance is a 0.10
1 - (
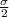 ) = 0.95.
) = 0.95.
The absolute value of z-critical is 1.645.
CI =
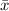 ±
±
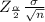
CI = 516 ± 1.645
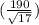
CI = 516 ± 75.8045
CI = (440.426, 591.574)
The mean number of tongue flicks every 20 minutes for all young common lizards falls within the interval, with a confidence level of about 90%.
Option a is the right choice.