Question

A collection of nickels and quarters are worth $2.85. There are 3 more nickels than quarters. How many nickels and quarters are there?

Answer 1

nickels = 12

quarters = 9

Explanation:

Let number of quarters be "q", and

number of nickels be "n"

Nickels are worth $0.05 and Quarters are worth $0.25

Since all of them are worth 2.85, we can write:

0.25q + 0.05n = 2.85

Also, we know, there are 3 more nickels than quarters, so we can write:

n = 3 + q

Now, we can substitute equation 2 into equation 1 to get:

`0.25q + 0.05n = 2.85\\0.25q + 0.05(3+q) = 2.85\\0.25q+0.15+0.05q=2.85`

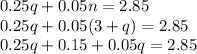
Now, we solve for q:

`0.25q+0.15+0.05q=2.85\\0.3q=2.70\\q=9`

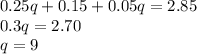
There are 9 quarters.

We know n = 3 + q

So,

n = 3 + 9

n = 12

There are 12 nickels