Question

When the displacement in SHM is equal to 1/2 of the amplitude xm, what fraction of the total energy is (a) kinetic energy and (b) potential energy? (c) At what displacement, in terms of the amplitude, is the energy of the system half kinetic energy and half potential energy? (Give the ratio of the answer to the amplitude)

Answer 1

Step-by-step explanation:

Let x₀ be the amplitude , ω be the angular velocity

velocity at displacement x ,

v = ω
`√((x_0^2-x^2))`

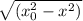
at
`x =(x_0)/(2)`

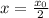
v = ω [
`\sqrt{(x_0^2-(x_0)/(4) ^2)}`

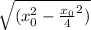
v² = ω² x
`(3x_0^2)/(4)`

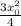
1/2 m v²

= 3/8 m x ω²x₀²

Total energy = 1/2 m ω²x₀²

Kinetic energy as fraction of total energy

= 3/8 m x ω²x₀² x 2 / m ω²x₀²

= 3 / 4

Fraction of potential energy

= 1 - 3/4

1/4

c )

Half kinetic = half potential energy

= 1/4 m ω²x₀²

1/2 m ω²( x₀²- x ² )

x₀²/2 = x₀²- x ²

x² = x₀²/2

x = x₀/√2