Answer:
0.9544
Explanation:
Let the measured resistances of the wire production by Company B = x
Define the standard normal variable
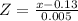
The probability that a randomly selected wire from Company B's production lot will meet the specification is :
P = (0.12 ≤ X ≤ 0.14)
=

=
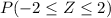
=
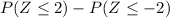
= 0.9772 - (1 - 0.9972)
= 0.9544