Answer:
(a)
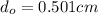 and (b)
and (b)
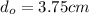
Step-by-step explanation:
The linear magnification (M) produced by a lens is giving by:
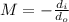 (1)
(1)
where
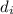 : is the image distance and
: is the image distance and
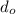 : is the object distance
: is the object distance
Knowing that the lens formula relates the focal length of an image with the distance of the image and the distance of the object:
 (2)
(2)
(a) To calculate the distance of the object, first we have to express the equation (1) in function of the image distance:
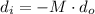 (3)
(3)
Finally, by the introducing
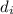 from (3) into equation (2) we can determine the distance of the object as follows:
from (3) into equation (2) we can determine the distance of the object as follows:
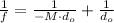
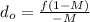 (4)
(4)
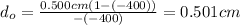
So the object needs to be placed at 0.501 cm from the microscope.
(b) To find the distance of the length eyepiece we will do the same treatment as before, to get to equation (4):
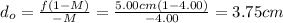
Have a nice day!