Question

The magnetic field in a region of space centered on the origin has cylindrical symmetry and is given by B~ = B0φˆ where B0 is a constant and φˆ is the azimuthal direction in cylindrical coordinates. What is the current density in this region of space?

Answer 1

To solve this problem, the application of the Ampere law is necessary.

This law relates the integrated magnetic field around a closed loop to the electric current passing through the loop.

The equation is defined as,

`\int Bdl=\mu_0J\pi r^2`

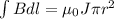
Where,

B= Magnetic field

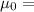`\mu_0 =`Permeability constant

J = Total current density

r = Radius

Integrating we have:

`B(2\pi r) = \mu_0 j\pi r^2`

`J = (2B)/(\mu_0 r)`

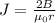
Therefore with that condition the previous equation represent the current density in this region of space