Question

Suppose the driving distance to work for residents of a certain community has a mean of 21 miles and a standard deviation of 3.6 miles. What is the probability that an individual drives between 19 and 26 miles to work? Assume that the distribution is normal

Answer 1

`P(19<X<26)=0.63`

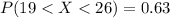
Explanation:

We start by defining the random variable X.

X : ''The driving distance to work for residents of a certain community''

X can be modeled as a normal random variable.

X ~ N (μ,σ)

Where μ is the mean and σ is the standard deviation.

For this problem :

X ~ N (21,3.6)

Where the unit for the mean and the standard deviation is miles.

We are looking for
`P(19<X<26)`

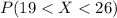
Given a normal random variable,we can subtract it the mean and then divide by the standard deviation in order to obtain a new random variable ''Z''.

Where ''Z'' is a new normal random variable.This is called standardizing.

Z ~ N (0,1)

The mean of Z is 0 and the standard deviation is 1.

We can find the cumulative probability distribution of Z in any table.

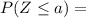`P(Z\leq a)=` Φ(a) given a certain value ''a''.

For the problem :

`P(19<X<26)=`

`P((19-21)/(3.6)<(X-21)/(3.6)<(26-21)/(3.6))=`

`P(-0.5555<Z<1.3888)=P(Z<1.3888)-P(Z<-0.5555)`

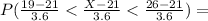
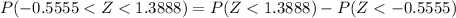
`P(19<X<26)=` Φ(1.3888) - Φ(-0.5555) = 0.9177 - 0.2877 = 0.63

The probability that an individual drives between 19 and 26 miles to work is 0.63