Question

The FMA Company has designed a new type of 16 lb. bowling ball. The company knows that the average man who bowls in a scratch league with the company's old ball has a bowling average of 155. The company asks a random sample of 120 men bowling in scratch leagues to bowl for five weeks with their new ball. The mean of bowling averages for these men with the new ball is 170. The variance is 100. If we want to test the null hypothesis that the new ball does not have the same bowler's average as the last ball using α=0.05, find the rejection region and test statistic of the necessary test to be hel?

Answer 1

Explanation:

Hello!

The FMA Company designed a new type of bowling ball and want to test if the new bowling average differs from the bowling average of the old model. Symbolically μ≠155

Sample:

n= 120 men bowling in scratch leagues

sample mean x[bar]= 170

variance δ²= 100

The hypothesis is:

H₀:μ=155

H₁:μ≠155

α: 0.05

The statistic to use for this hypothesis, assuming that the variable has a normal distribution.

Z= x[bar]-μ ≈ N(0;1)

δ/√n

The critical region for this test is two-tailed, this means you'll reject the null hypothesis to small or big values of the statistic.

`Z_(\alpha/2)` =
`Z_(0.025)` = -1.96

`Z_(1-\alpha/2)` =
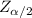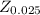`Z_(0.975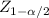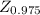)` = 1.96

You'll reject the null hypothesis to values of Z≤-1.96 or Z≥1.96.

Under the null Hypothesis the statistic value is:

Z= x[bar]-μ

δ/√n

Z= 170-155

10/√120

Z= 15/0.913 = 16.42

Decision: Reject the null Hypothesis.

I hope you have a SUPER day!