Question

Delaney would like to make a 10 lb nut mixture that is 60% peanuts and and 40% almonds. She has several pounds of peanuts and several pounds of a mixture that is 20% peanuts and 80% almonds. Let p represent the number of pounds of peanuts needed to make the new mixture, and let m represent the number of pounds of the 80% almond-20% peanut mixture.

(a) What is the system that models this solution?
(b) Which of the following is a solution to the system: 4 lb peanuts and 6 lb mixture; 5 lb peanuts and 5 lb mixture; 8 lb peanuts and 2 lb mixture? Show your work.

Answer 1

If there is "p" pounds of peanuts and "m" pounds of '20% peanuts and 80% almonds' mixture, then, we can get the following equations,

p + m = 10 -----------(1) and

4m/5 = 4 ------------(2)

whose solution is 5 lb peanuts and 5 lb mixture.

Explanation:

In the mixture which Delaney wants to make there would be

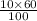`\frac {10 * 60}{100}` lb

= 6 lb of peanuts

So, there will be (10 - 6) lb

= 4 lb of almonds

If Delaney has "p" pounds of peanuts and "m" pounds of the '20% peanuts and 80% almonds' mixture, then according to the question,

p + m = 10 -----------(1) and

4m/5 = 4 ------------(2)

So, from (2),

m = 5 --------------(3)

So, from (1) and (3) ,

p = (10 - 5) = 5