Answer:
There are no real values of y for which g'(y) is undefined.
Explanation:
We are given the following in the question:
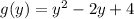
We have to find values for which g'(y) is undefined.
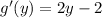
Putting g(y) = 0, we get:

Since those are not real numbers, there are no real numbers where g'(y) is undefined.
Thus, there are no real values of y for which g'(y) is undefined.