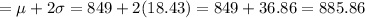Answer:
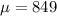

Minimum usual value
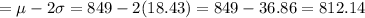
Maximum usual value
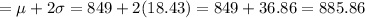
Explanation:
The Normal approximation can be used to binomial distribution, when n is large and p is near to 0.5.
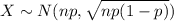
here, Mean =
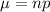
Standard deviation :
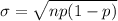
Given :
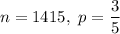
Then,
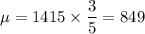

Range rule of thumb : It says that the range is approximately four times the standard deviation.
Minimum usual value
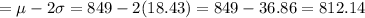
Maximum usual value