Question

A thin layer of oil with index of refraction no = 1.47 is floating above the water. The index of refraction of water is nw = 1.3. The index of refraction of air is na = 1. A light with wavelength λ = 450 nm goes in from the air to oil and water. Express the minimum thickness of the film that will result in destructive interference, tmin, in terms of λ.

Answer 1

To solve this exercise it is necessary to apply the concepts related to destructive interference. Destructive interference occurs when the maxima of two waves are 180 degrees out of phase: a positive displacement of one wave is canceled exactly by a negative displacement of the other wave. The amplitude of the resulting wave is zero.

From the image we can realize that the minimum thickness would be half the wavelength, i.e, because oil has a higher index of refraction than air, the wave reflecting off the top surface of the film is shifted by half a wavelength.

`t_(min) = (\lambda_0)/(2)`

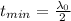
Where,

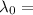`\lambda_0 =`Wavelength of light