Answer:
The given expression can't be expressed in polynomial form. Hence, it is not a polynomial.
Explanation:
P(x,n) is a polynomial of nth degree if it is of the form,
P(x,n) =
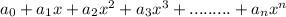
where n is a finite positive integer and n ∈ N
and '
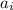 's are fixed but otherwise arbitrary constants ∀ i = 0(1)n .
's are fixed but otherwise arbitrary constants ∀ i = 0(1)n .
Now, the given expression is,
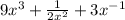
which doesn't fit in the above form. Hence, it is not a polynomial.