Answer:dy/dt(x=3)=54
Explanation:
We know that we can write:
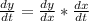
and so evaluate it as a product of functions, that is for a given value of x or t, we get that
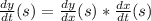 .
.
Now we are told that:
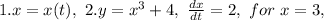
whenever it happens, this means the influence of t is hidden, and we only consider the result, that is, how much is x when the derivative has the value of 2, we are not concerned for what value of t it happens, since we get all the necessary information beforehand.
Now we need to calculate
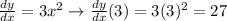 .
.
Therefore
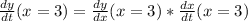 or
or
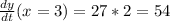 .
.