Answer:
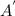 = (1,
= (1,
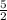 ),
),
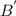 = (
= (
 ,-1) and
,-1) and
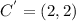
OA =
![\sqrt[]{29}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2t19gus21dh7jfh4a601pw30dqroigfqsl.png) units, OB =
units, OB =
![\sqrt[]{13}](https://img.qammunity.org/2020/formulas/mathematics/high-school/p22jmz2h182opd6g65xvfuq1cpw878op3w.png) units and OC =
units and OC =
![\sqrt[]{32}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9z7s8uvaudyi0adp84hqnqcazz87hlvleo.png) units
units
O
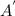 =
=
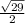 units,
units,
O
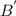 =
=
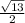 units and
units and
O
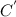 =
=
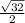 units
units
Explanation:
Given vertices are A(2,5), B(3,-2), C(4,4) and the new vertices after dilation are
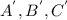
a.
Triangle needs to be dilated about the origin.
⇒The centre of dilation is the origin O(0,0).
scaling factor is

 =
=
 =
=
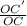 =
=

⇒
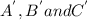 divide OA, OB and OC in the ratio 1:1 respectively.
divide OA, OB and OC in the ratio 1:1 respectively.
Using the formula for the coordinates of a point dividing two points (0,0), (x,y) in the ratio 1:1 is (
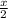 ,
,
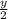 ) :
) :
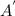 = (1,
= (1,
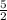 ),
),
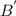 = (
= (
 ,-1) and
,-1) and
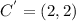
b.
Using the formula for the distance between the points (0,0) and (x,y) is
![\sqrt[]{x^(2 )+ y^(2) }](https://img.qammunity.org/2020/formulas/mathematics/high-school/o9wd1ygtqhlxl80f8ropfg1gawpxvaprfa.png) :
:
OA =
![\sqrt[]{2^(2) +5^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/m00ovp3dsux4jql5muromf25sdhw4m0o6l.png) =
=
![\sqrt[]{29}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2t19gus21dh7jfh4a601pw30dqroigfqsl.png) units
units
OB =
![\sqrt[]{3^(2) +-2^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/qkaxxf1xyeyel1bifwbjf93byilredf7d5.png) =
=
![\sqrt[]{13}](https://img.qammunity.org/2020/formulas/mathematics/high-school/p22jmz2h182opd6g65xvfuq1cpw878op3w.png) units
units
OC =
![\sqrt[]{4^(2) +4^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/fphndjxwzzdy3vlt1lxzflt2j846q90jpv.png) =
=
![\sqrt[]{32}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9z7s8uvaudyi0adp84hqnqcazz87hlvleo.png) units
units
c.
From the property of dilation :
 =
=
 =
=
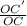 =
=

⇒O
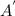 =
=
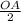 =
=
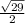 units
units
O
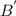 =
=
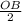 =
=
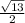 units
units
O
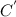 =
=
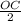 =
=
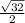 units
units
d.
Using the formula for the distance between two points :
O
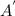 =
=
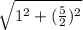 =
=
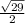 units
units
O
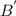 =
=
 =
=
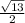 units
units
O
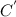 =
=
![\sqrt[]{2^(2) +2^(2)}](https://img.qammunity.org/2020/formulas/mathematics/high-school/nixfwr6lxioaodbxjw3pwb0h2dm4udo1z3.png) =
=
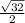 units
units
which are the same as we predicted in part c.