Question

What is the area of this triangle? Enter your answer as a decimal in the box. Round only your final answer to the nearest hundredth. ft² The figure contains a triangle. One side is 2.7 feet. A second side is 3.4 feet. The angle between the given sides is 40 degrees.

Answer 1

The area of triangle is
`3.42 \mathrm{ft}^(2)`

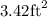
Step-by-step explanation:

We are given two sides of a triangle and their including angle.

The two given sides of a triangle are , one is 2.7 ft and other is 3.4 ft

And the including angle is given to be 40°

The formula to find area of triangle when two sides and their including angle is given is-

=
`(a b \sin \theta)/(2)`

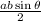
where a and b are two sides and θ is the including angle.

Substituting the given values,

Area =
`(2.7 * 3.4 * \sin 40^(\circ))/(2)`

=
`(2.7 * 3.4 * 0.74)/(2)`

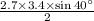
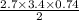
= 3.42

Hence
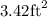`3.42 \mathrm{ft}^(2)` is the area of triangle.

Answer 2

Area of the triangle
`\simeq` 5.9 sq. ft. .

Step-by-step explanation:

Length of two sides of the triangle are, 2.7 feet and 3.4 feet and the angle between them is 40° .

So, the area of the triangle is given by,

`2.7 * 3.4 * \sin {40^(\circ)}` sq. ft.

`\simeq 5.9` sq. ft.