Answer:
Here is the complete question (attachment).
The function which represent the given points are
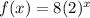
Explanation:
We know that a general exponential function is like,
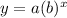
We can find the answer by hit and trial method by plugging the values of
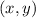 coordinates.
coordinates.
Here we are going to solve this with the above general formula.
So as the points are
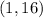 then for
then for

Can be arranged in terms of the general equation.
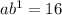 ...equation(1) and
...equation(1) and
 ...equation(2)
...equation(2)

Plugging the values in equation 2.
We have
![(16)/(b) b^4=128,16* b^3=128,b=\sqrt[3]{(128)/(16)} =\sqrt[3]{8}=2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lvxz25c06sejy8c8ed7jvoyupnz60tn1hd.png)
Plugging
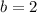 in equation 1.
in equation 1.
We have
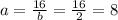
Comparing with the general equation of exponential
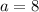 and
and
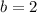
So the function which depicts the above points =
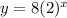
From theoption we have B as the correct answer.