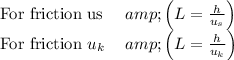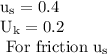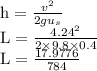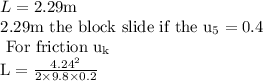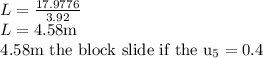Question

A 2 kg block is pushed against a spring (k = 400 N/m), compressing it 0.3 m. When the block is released, it moves along a frictionless, horizontal surface, and then up an incline that has friction (μs = 0.4 and μk = 0.2). How far up the incline does the block slide before coming to rest?

Answer 1

`2.29 \mathrm{m} \text { the block slide if the } \mathrm{u}_{\mathrm{s}}=0.4`

`4.58 \mathrm{m} \text { the block slide if the } \mathrm{u}_{\mathrm{k}}=0.2`

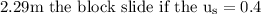
Step-by-step explanation:

Given values

Mass (m) = 2kg

K = 400 N/M

Compressing it 0.3 m

The law of conservation of energy:

`(m v^(2))/(2)+(k x^(2))/(2)=\text { constant }`

`\text { Where, } (m v^(2))/(2) \text { is kinetic energy of the block. }`

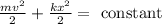
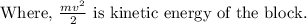
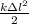`(k \Delta l^(2))/(2)` Energy of the spring deformation.

M mass of the block

x spring deformation

Therefore, if block left the spring (x = 0)

`(m v^(2))/(2)+0=0+(k \Delta l^(2))/(2)`

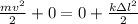
Where, Δl is initial spring deformation

`(m v^(2))/(2)=(k \Delta l^(2))/(2)`

`\mathrm{v}^(2)=(k \Delta l^(2))/(m)`

`\mathrm{v}=\sqrt{(k)/(m) * \Delta l^(2)}`

`v=\sqrt{(400)/(2) *(0.3)^(2)}`

`\mathrm{v}=√(200 * 0.09)`

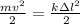
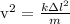
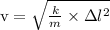
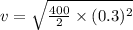
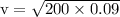
The law of conservation of energy:

`(m v^(2))/(2)+m g h=\text { constant }`

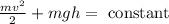
Where h is height

`(m v^(2))/(2)+0=0+m g h`

`(m v^(2))/(2)=m g h`

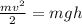
Cancel mass "m" each side

`\mathrm{h}=(v^(2))/(2 g)`

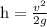
Distance along incline equals

`\begin{array}{ll}{\text { For friction us }} & {\left(L=(h)/(u_(s))\right)} \\ {\text { For friction } u_(k)} & {\left(L=(h)/(u_(k))\right)}\end{array}`

`\begin{array}{l}{\mathrm{u}_{\mathrm{s}}=0.4} \\ {\mathrm{U}_{\mathrm{k}}=0.2} \\ {\text { For friction } \mathrm{u}_{\mathrm{s}}}\end{array}`

`\begin{array}{l}{\mathrm{h}=(v^(2))/(2 g u_(s))} \\ {\mathrm{L}=(4.24^(2))/(2 * 9.8 * 0.4)} \\ {\mathrm{L}=(17.9776)/(784)}\end{array}`

`\begin{array}{l}{L=2.29 \mathrm{m}} \\ {2.29 \mathrm{m} \text { the block slide if the } \mathrm{u}_(5)=0.4} \\ {\text { For friction } \mathrm{u}_{\mathrm{k}}} \\ {\mathrm{L}=(4.24^(2))/(2 * 9.8 * 0.2)}\end{array}`

`\begin{array}{l}{L=(17.9776)/(3.92)} \\ {L=4.58 \mathrm{m}} \\ {4.58 \mathrm{m} \text { the block slide if the } \mathrm{u}_(5)=0.4}\end{array}`