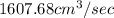Answer:
So rate of pump after t =4 sec will be
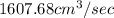
Step-by-step explanation:
We have given that volume of the sphere
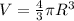
It is given that at after t sec radius of the sphere is 2t cm
So volume of the sphere
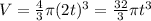
After differentiating
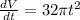
We have to find the rate of pump at t = 4 sec
So
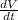 at t = 4 sec
at t = 4 sec
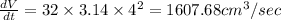
So rate of pump after t =4 sec will be