Question

The incomes in a certain large population of high school teachers has a mean income μ=$70,000 and standard deviation σ=$6,000, 50 teachers are selected at random from this population for a survey. a) Based on the central limit theorem we would expect the distribution of the sample mean incomes to be approximately b) What is the mean of the sampling distribution of the mean (x)? c) What is the standard deviation of the sampling distribution of the mean ()? (1 decimal place) d) What is the probability that the average salary of the 50 teachers is more than $72,000?

Answer 1

Explanation:

Hello!

Your study variable is X: "Income of a high school teacher"

μ=$70,000

σ=$6,000

n= 50 teachers

a. The Central Limit Theorem states that if you have a variable of unknown distribution (or known but not normal distribution), if a big enough sample if taken (normally with n≥30), you can aproximate the distribution of the sample mean to normal, symbolically:

X[bar]≈N(μ;δ²/n)

b. The population mean of the sampling distribution, is the same as the population mean of the study variable. In this example μ=$70,000.

c. The standard deviation of the sampling distribution is √(δ²/n), calculated is 6000/√50 = $848.528 ≅ $848.53

d. P(X[bar]>72000) = 1 - P(X[bar]≤72000)

⇒ 1 - P(Z ≤
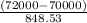`((72000-70000))/(848.53)`) = 1 - P(Z ≤ 2.36) = 1 - 0.9909 = 0.0091

The formula for the standarization is Z= X[bar] - μ ≈ N(0;1)

δ/√n

I hope it helps!