Answer:
The other leg of the triangle is 12.
Explanation:
Given:
Hypotenuse of triangle is 13 and a leg(Leg1) is 5.
Let, the other leg of the triangle (Leg2) be
 .
.
Now, putting the formula:
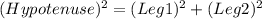
⇒
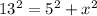
⇒
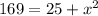
⇒
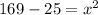
⇒
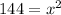
Taking square root both sides
⇒
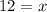
⇒
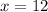 .
.
Therefore, the other leg of the triangle is 12.