Question

If a die is rolled 40 times, there are 640 different sequences possible. The following question asks how many of these sequences satisfy certain conditions. HINT [Use the decision algorithm discussed in Example 3 of Section 6.3.] What fraction of these sequences have exactly five 1s? (Round your answer to four decimal places.)

Answer 1

0.1433

Explanation:

All possibilities:

The total number of different sequences in 40 rolls of a die is
`6^(40)`

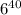
Exactly five 1s in 40 rolls:

The 1s may occur at any 5 rolls among 40. The number of ways of exactly five 1s occuring is therefore, equivalent to number of ways of selecting 5 fruits from 40 distinct fruits which is ⁴⁰C₅ ways. These 5 rolls have a fixed outcome 1. Other 35 rolls each have 5 possible outcomes : 2 or 3 or 4 or 5 or 6. So, the number of possible sequences of outcomes on other 35 rolls of the die is
`5^(35)`.

⇒The total number of different sequences having exactly five 1s in 40 rolls of a die is (⁴⁰C₅)×(
`5^(35)`)

∴The fraction of the total number of sequences having exactly five 1s is
)}{
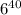`6^(40)`}[/tex] ≈ 0.1433