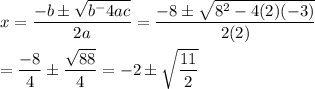Answer:
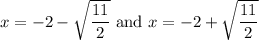
Explanation:
My favorite way to go at this is to look at a graph. It shows the vertex at (-2, -11). Since the leading coefficient is 2, this means the roots are ...
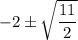
where the 2 in the denominator of the radical is the leading coefficient.
__
You can also use other clues:
- the axis of symmetry is -b/(2a) = -8/(2(2)) = -2, so answer choices C and D don't work
- the single change in sign in the coefficients (+ + -) tells you there is one positive real root, so answer choice B doesn't work.
The first answer choice is the only one with values symmetrical about -2 and one of them positive.
__
You may be expected to use the quadratic formula: