Question

The height of a triangle is 4 sqrt 3 . What is the perimeter of the equatorial triangle?

Answer 1

The perimeter of the equatorial triangle is 24 units

Solution:

Given that,

An equilateral triangle has an height equal to
`4 √(3)`

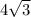
The triangle is shown below

From Triangle ABC in the shown figure AD
`=4 √(3)`

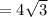
Let the sides of the equilateral triangle be ‘a’

AB = BC = a

Since, it is an equilateral triangle we get,

BD = DC = a ÷ 2

Now, using Pythagoras Theorem in Triangle ABD,

The Pythagorean theorem is this: In a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse.

`\mathrm{AB}^(2)=\mathrm{BD}^(2)+\mathrm{AD}^(2)`

`\begin{array}{l}{a^(2)=\left((a)/(2)\right)^(2)+(4 √(3))^(2)} \\\\ {a^(2)-\left((a)/(2)\right)^(2)=(4 √(3))^(2)}\end{array}`

`(4 a^(2)-a^(2))/(4)=16 * 3`

`\begin{array}{l}{(3 a^(2))/(4)=16 * 3} \\\\ {3 a^(2)=192} \\\\ {a^(2)=192 / 3=64}\end{array}`

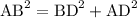
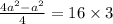
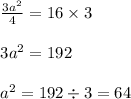
a = 8

Hence, the three sides of the triangle are 8 units each

In equilateral traingle, length of all three sides of triangle are equal

So, Perimeter = 3
`*` (Length of each side of triangle)

Perimeter = 3
`*` 8 = 24

Thus the perimeter of the equatorial triangle is 24 units