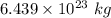Question

Phobos orbits Mars in 27,553 s at a distance of 9.378 × 106 m. What is the mass of Mars? 2.58 × 1011 kg 2.05 × 1023 kg 6.43 × 1023 kg 1.09 × 1030 kg

Answer 1

Answer is C. I just took it E2020

Step-by-step explanation:

Answer 2

6.43
`*`
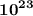`\textbf{10}^\textbf{23}` kg

Step-by-step explanation:

Phobos orbits Mars in a circular path. So, there must some force acting as centripetal force to maintain the circular path. Gravitational force due to mars takes this role of Centripetal Force.

So, Gravitational Force = Centripetal Force

`(GMm)/(r^(2)) =(mv^(2))/(r)`

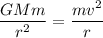
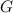`G` is the Gravitational constant,
`M` is the mass of Mars,
`m` is the mass of Phobos,
`v` is the velocity of Phobos,
`r` is the Radius of orbit,
`T` is the Time period.

`v=\frac{Circumference}{Time\text{ }Period}=(2\pi r)/(T)\\\\(GMm)/(r^(2))=(m* ((2\pi r)/(T))^(2))/(r)\\\\ (GM)/(r)=(4\pi^(2)r^(2))/(T^(2))\\\\G=6.67*10^(-11)\text{ }m^(3)kg^(-1)s^(-2),\text{ }r=9.378*10^(6)\text{ }m,\text{ }T=27533\text{ }sec\\M=(4\pi^(2)* (9.378*10^(6))^(3))/((27533)^(2)* (6.67*10^(-11)))= 6.439*10^(23)\text{ }kg`

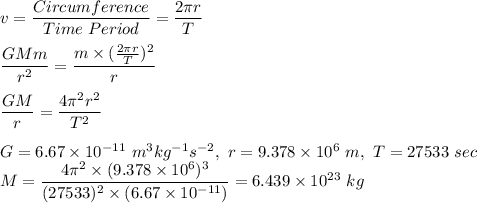
∴ Mass of Mars =
`6.439*10^(23)\text{ }kg`