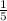Question

What is the value of y in the following system y=3x-7 6x+3y=15

Answer 1

For this case we have the following system of equations:

`y = 3x-7\\6x + 3y = 15`

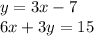
To find the solution, we follow the steps below:

We substitute the first equation in the second equation:

`6x + 3 (3x-7) = 15\\6x + 9x-21 = 15\\15x = 15 + 21\\15x = 36\\x = \frac {36} {15}\\x = \frac {12} {5}`

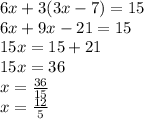
Now, we find the value of "y":

`y = 3 (\frac {12} {5}) - 7\\y = \frac {36} {5} -7\\y = \frac {36-35} {5}\\y = \frac {1} {5}`

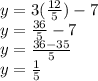
Thus, the solution of the system is:

`(x, y): (\frac {12} {5}, \frac {1} {5})`

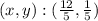
Answer:

The value of the variable "y" is
`\frac {1} {5}`