Question

One way that future space stations may create artificial gravity is by rotating the station. Consider a cylindrical space station 380 m in diameter that is rotating about its longitudinal axis. Astronauts walk on the inside surface of the space station. How long will it take for each rotation of the cylinder if it is to provide normal gravity for the astronauts?

Answer 1

27.65 sec

Step-by-step explanation:

The Cylinder rotates about it's axis, thus there exists a Centrifugal force on a object which is on the inner surface of the cylinder. This is one of the many ideas that are currently being used in space habitation.

So, Centrifugal force acts like Normal gravity when both have equal magnitude.

`F_(c)=(mv^(2))/(r)=F_(g)=mg`

`m` is the mass of astronaut,
`g` is the Earth's gravity,
`v` is the velocity of astronaut,
`T` is the Time period of rotation.

`v=(2\pi r)/(T)`

`g=(v^(2))/(r)=(((2\pi r)/(T))^(2))/(r) =(4\pi^(2)r)/(T^(2))`

`g=9.81\text{ }(m)/(s^(2)),\text{ }r=190\text{ }m`

`T^(2)=(4\pi^(2)(190))/(9.81)= 764.6177\text{ }sec^(2)\\\\T=27.65\text{ }sec`

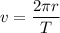
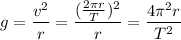
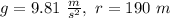
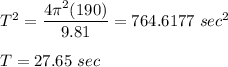
∴ It takes 27.65 sec for rotation of cylinder, if it is to provide normal gravity for astronauts.