To develop the problem it is necessary to apply the concepts of Volume calculation, area calculation and the solidification time.
The solidification time equation is given by
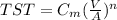
Where,
TST = Total solidification time
V = Volume of the casting
A = Surface area of casting
n = Exponent with typical value=2
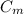 = Mold constant
= Mold constant
We do not have the volume or area, so we proceed to calculate them with the data we have,
Volume,
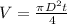

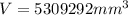
Area,

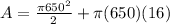
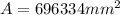
Replacing at the previous equation we have
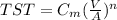
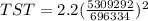
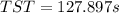
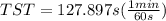

Therefore it will take the casting to solidify around to 2.13min