Question

A 200-kilogram tool box is hoisted by a rope from the ground to the roof of an apartment building 20 meters above the ground. The rope has a density 2 kg/m. Find the work done in lifting the tool box from the ground to the roof.

Answer 1

Total Work Done = 39600 N

Explanation:

This problem involves a tool box and a rope used to pull the tool box.

So the work done will be calculated in two parts:

1) Work done on Tool Box

2) Work done on Rope

1)Work done on Tool Box:

mass of tool box = m= 200 kg

Force = F = mass x gravity = mg = 200 x 9.8

F= 1960 N

distance = d = 20m

Now,We will use formula of work done:

Work done = Force x Distance = F x d

Work Done = W = 1960 x 20

Work done on Box= 39200 N ----------------------- Eq. 1

2) Work done on rope:

Here we will consider that the rope has infinitesimally small parts namely Δx and after pulling the rope at a certain random length , we call it
`x_(i)`

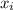
We can represent it using the work done formula in limits :

Work Done =
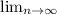`\lim_(n \to \infty)` ∑ ρ Δx
`x_(i)`

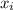
(Note : For ∑, its is from 1 to Infinity)

(Note : ρ is the density of rope)

ρ = density of rope = 2 kg/m

We can further write it in integral form as :

Work done on rope = W =
`\int\limits^d_0 {2 x} \, dx`

After integration :

W=
`(2)/(2)`
`x^(2)`
`\left \| {{20} \atop {0}} \right.`

W =
`20^(2) - 0`

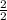
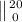
W= 400N ----------------------------------------(Eq .2)

Which is the work done on rope

Total Work done = Work done on rope + Work done on tool box

Total Work Done = 400 + 39200

Total Work Done = 39600 N