Question

1. Write an inequality for the range of the third side of a triangle if two sides measure 4 and 13.

2. If LM = 12 and NL = 7 of ∆LMN, write an inequalty to describe the lenght of MN.


3. Use the Hinge Theorem to compare the measures of AD and BD.

Answer 1

Part 1) The inequality for the range of the third side is
`9 < x < 17`

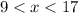
Part 2) The inequality to describe the length of MN is
`5 < MN < 19`

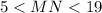
Part 3) AD is longer than BD (see the explanation)

Explanation:

Part 1) we know that

The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side.

Let

x ----> the measure of the third side of a triangle

so

Applying the triangle inequality theorem

a) 4+13 > x

17 > x

Rewrite

x < 17 units

b) x+4 > 13

x > 13-4

x > 9 units

therefore

The inequality for the range of the third side is equal to

`9 < x < 17`

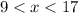
Part 2) we know that

The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side.

Let

x ----> the measure of the third side of a triangle

so

Applying the triangle inequality theorem

a) LM+NL > MN

12+7 > MN

19 > MN

Rewrite

MN < 19 units

b) MN+NL > LM

MN+7 > 12

MN > 12-7

MN > 5 units

therefore

The inequality to describe the length of MN is

`5 < MN < 19`

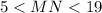
Part 3) we know that

The hinge theorem states that if two triangles have two congruent sides, then the triangle with the larger angle between those sides will have a longer third side

In this problem Triangles ADC and BCD have two congruent sides

AC≅BC

DC≅CD ---> is the same side

The angle between AC and CD is 70 degrees

The angle between BC and CD is 68 degrees

Compare

70° > 68°

therefore

AD is longer than BD