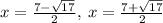Question

Use the quadratic formula to solve the equation. –x2 + 7x = 8

Answer 1

The solutions are:

`x=(7-√(17))/(2),\:x=(7+√(17))/(2)`

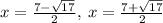
Explanation:

Given the quadratic equation

-x² + 7x = 8

Solving using the quadratic formula

`-x^2+7x=8`

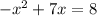
Subtract 8 from both sides

`-x^2+7x-8=8-8`

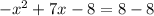
Simplify

`-x^2+7x-8=0`

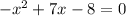
For a quadratic function of the form ax² + bx + c = 0, the solutions are:

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

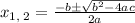
For a = -1, b = 7, c = -8

`x_(1,\:2)=(-7\pm √(7^2-4\left(-1\right)\left(-8\right)))/(2\left(-1\right))`

`x_(1,\:2)=(-7\pm \:√(49-32))/(2\left(-1\right))`

`x_(1,\:2)=(-7\pm √(17))/(2\left(-1\right))`

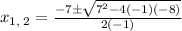
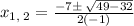
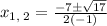
Separate the solutions

`x_1=(-7+√(17))/(2\left(-1\right)),\:x_2=(-7-√(17))/(2\left(-1\right))v`

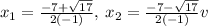
solving

`x_1=(-7+√(17))/(2\left(-1\right))`

`=(-7+√(17))/(-2)`

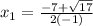
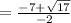
Apply the fraction rule:
`(-a)/(-b)=(a)/(b)`

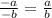
i.e.
`-7+√(17)=-\left(7-√(17)\right)`

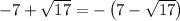
so

`=(7-√(17))/(2)`

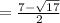
Similarly solving

`x_2=(-7-√(17))/(2\left(-1\right))`

`=(-7-√(17))/(-2\cdot \:1)`

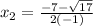
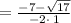
Apply the fraction rule:
`(-a)/(-b)=(a)/(b)`

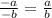
i.e.
`-7-√(17)=-\left(7+ √(17)\right)`

`=(7+√(17))/(2)`

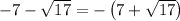
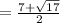
Therefore, the solutions are:

`x=(7-√(17))/(2),\:x=(7+√(17))/(2)`