Answer: Length of one leg =x = 11.3 m
Length of another leg = 11.3-3 = 8.3 m
Explanation:
Let one leg of the right triangle be x , then the other leg be x-3.
Hypotenuse = 14 meters
- Pythagoras theorem of right -triangle says that he square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.
Then for the given situation , we have
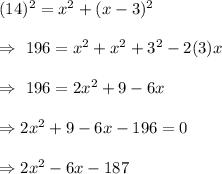
Which is a quadratic equation.
For quadratic equation
 , the root of equation is
, the root of equation is
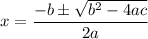
In
 , a= 2 , b= -6 and c=-187 , then
, a= 2 , b= -6 and c=-187 , then
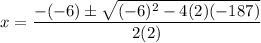
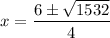
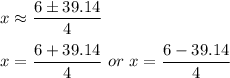
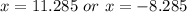
Side cannot be negative , so avoid x=-8.285.
so

⇒ Length of one leg =x = 11.3 m
Length of another leg = 11.3-3 = 8.3 m