Question

Find the value of "x" from the given figure...

`....................`
​

Answer 1

21 cm

Explanation:

Let M be the point of intersection of the diagonals AD and BC.

`\implies x=\sf AD=AM+MD`

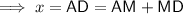
As ΔAMD and ΔBMD are right triangles, use Pythagoras Theorem to work out the lengths of AM and MD.

Pythagoras Theorem

`a^2+b^2=c^2`

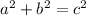
where:

• a and b are the legs of the right triangle.
• c is the hypotenuse (longest side) of the right triangle.

`\begin{aligned}\implies \sf BM^2+AM^2 & =\sf AB^2\\\sf 8^2+AM^2 & = \sf 10^2\\\sf 64+AM^2 & = \sf 100\\\sf AM^2 & = \sf 100-64\\\sf AM^2 & = \sf 36\\\sf AM & = \sf √(36)\\\sf AM & = \sf 6\:\: cm\end{aligned}`

`\begin{aligned}\implies \sf BM^2+MD^2 & =\sf BD^2\\\sf 8^2+MD^2 & = \sf 17^2\\\sf 64+MD^2 & = \sf 289\\\sf MD^2 & = \sf 289-64\\\sf MD^2 & = \sf 225\\\sf MD& = \sf √(225)\\\sf MD& = \sf 15\:\: cm\end{aligned}`

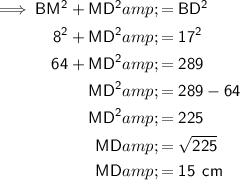
Therefore:

`\begin{aligned}\implies x & =\sf AM+MD\\x & = \sf 6+15\\x & = \sf 21\:\:cm\end{aligned}`

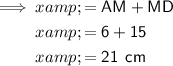
So the value of
`x` from the given figure is 21 cm.

Answer 2

x = 21 cm

Explanation:

is a rhombus formed by 4 right triangles, let's consider the small / large couple

the triangle at the top and the triangle at the bottom are rectangles

we can solve with the Pythagorean theorem.

• we find the side (cathetus) of the small one

c² = 10² - 8²

c² = 100 - 64

c² = 36

c = √36

c = 6 cm

• we find the side (cathetus) of the largest

c² = 17² - 8²

c² = 289 - 64

c² = 225

c = √225

c = 15 cm

• now we add the results and we have x

6 + 15 =

21cm