Answer:
The value of given log function is 1 .
Explanation:
Given as :
Logb A = 3
Logb C = 2
Logb D = 5
Now from log property
if , Logb x = c , then x =
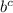
So,
Logb A = 3 , then A =
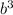
Logb C = 2 , then C =
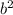
Logb D = 5 , then D =
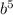
Now, According to question
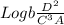
So,
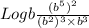
Or,
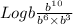
or,

Now, since base same So,

∴
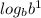
Now log property
 = 1
= 1
Hence The value of given log function is 1 . answer